| Current State | Symbol | New State |
| Start | x | Q1 |
| Start | y | Q2 |
| Start | z | Q3 |
| Q1 | x | Q1 |
| Q1 | y | Q3 |
| Q1 | z | Q2 |
| Q2 | x | Q3 |
| Q2 | y | Q2 |
| Q2 | z | Q1 |
| Q3 | x | Q1 |
| Q3 | y | Q2 |
| Q3 | z | Accept |
| Accept | x | Accept |
| Accept | y | Q1 |
| Accept | z | Q3 |
Sample solution |
(i) what would be the key states?
(ii) when would the transitions between them take place?
(iii) in which state(s) would the IR be updated?
(iv) in which state(s) might the PC be updated?
Sample solution
One simple possibility is to have five states:
start --> fetch --> decode --> execute --> accept
^ /
\__________________/
We go from start to fetch once the program is loaded and begins running,
we go from fetch to decode once the next instruction has been fetched,
we go from decode to execute once decoding is completed,
we go from execute to accept after a halt instruction has been executed,
otherwise once an instruction execution completes we go back to fetch
The instruction register would be updated during the fetch instruction.
The program counter would be updated during decoding,
but could also be updated by certain instructions during execution
(e.g. by a jump instruction).
|
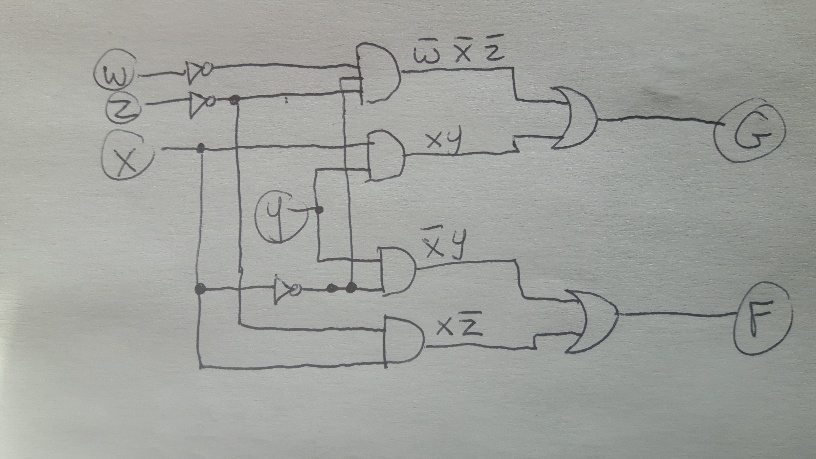
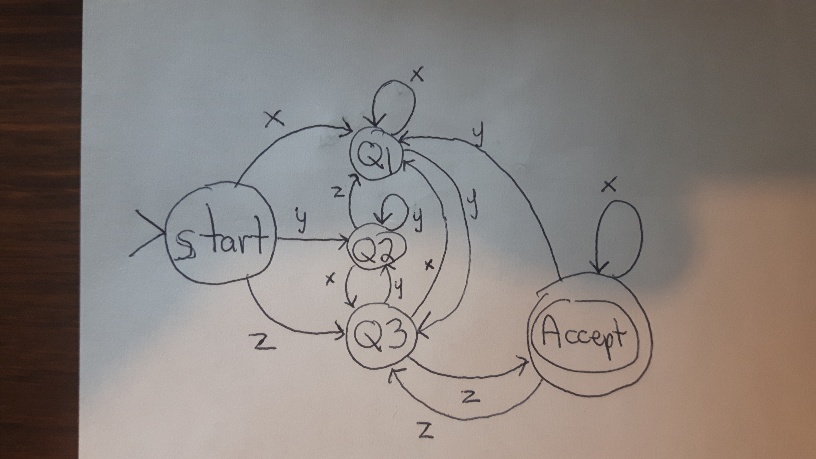 For string xyzyxxx the state sequence would be
Start -> Q1 -> Q3 -> Accept -> Q1 -> Q1 -> Q1 (string not accepted)
For string xyzyxxx the state sequence would be
Start -> Q1 -> Q3 -> Accept -> Q1 -> Q1 -> Q1 (string not accepted)
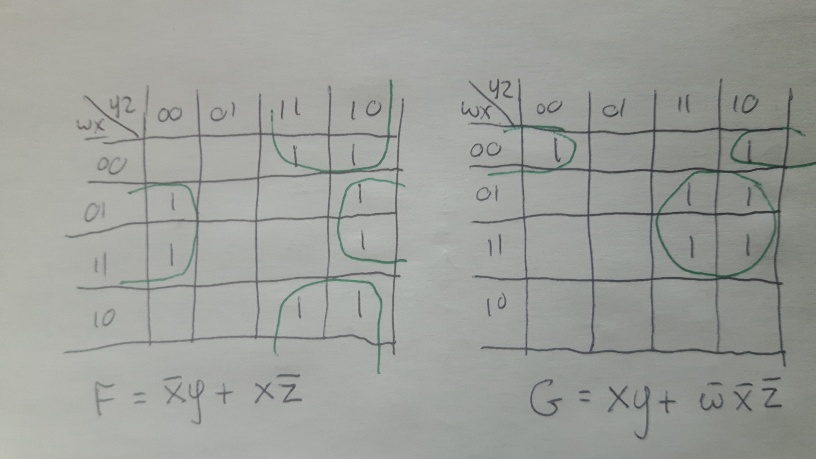 Remember the maps wrap around top-bottom and left-right,
hence for F we're getting three groups of four,
while for G we're getting a group of 2 and a group of 4
Remember the maps wrap around top-bottom and left-right,
hence for F we're getting three groups of four,
while for G we're getting a group of 2 and a group of 4